Transporte de energia en estado no estacionario con gradientes (coordenadas cartesianas)

Los fenómenos de transporte son aquellos procesos en los que hay una transferencia neta o transporte de materia en este caso el de energía o Estos fenómenos físicos tienen ciertos factores comunes que pueden ser descritos mediante la ecuación para la propagación unidimensional.

Esto nos permite tener lo perfiles de temperatura los cuales cambien con respecto al tiempo

La ecuación que describe la conducción térmica se conoce como ley de Fourier, en este caso el campo Ψ es la temperatura T, y el coeficiente α=K/(ρc), donde K, es la conductividad térmica, ρ la densidad, y c es el calor específico del material. La conducción del calor se establece siempre que exista un gradiente o diferencia de temperaturas entre dos puntos

La ecuación de difusión describe la conducción de calor en estado no estacionario, cuando no hay fuentes internas de generación de calor esta dada por:

Esta es la parte que nos interesa debido a que teniendo las condiciones de frontera Esta ecuación representa una gran familia de fenómenos. Para aplicarla a la solución de un caso particular es necesario fijar la, Geometría (Rectangular,  cilíndrica, esfera)

En una dimensión:

O de manera adimensinal:

Tenemos diferente métodos de aplicación y resolución de este estado las aplicadas son

-Separación de variables (unas pocas geometrías simples)

-Diferencias finitas y elemento finito

-De libros como Geankoplis

- graficar soluciones obtenidas analíticamente en excel

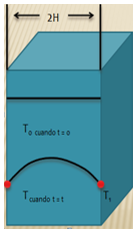
Solución de placa 2H

Condición Inicial

T = T0   en   t = 0   y   x = x

Condiciones a la frontera.

T = T1   en   t = t    y   x = 0

Condiciones a la frontera.

 T = T1   en   t = t    y   x = 2H

Se propone una solución de la forma:

Se realiza la derivada temporal:

Se realiza la derivada espacial:

Se sustituye dentro de la ecuación de difusión

Se divide entre T(x,t) = X(x) Ʈ(t)

Como ambas ecuaciones dependen de variables diferentes, deben ser -ambas- iguales a una constante

Lo que lleva al sistema de ecuaciones

Por este método de separación de variables encontramos

La solución particular es

Una ecuación en derivadas parciales de 2do orden se transformó en un sistema de dos ecuaciones ordinarias existiendo un número infinito de valores de λ para los que se cumplen las condiciones de frontera.

Cada uno de esos valores se llama valor propio (Eigen valor) y se denota λ_m